SISTEM PERSAMAAN LINEAR
Nama : Farahdiba soumena
Nim :202231006
Kelas : A
Jurusan : Teknik informatika
Tugas : Aljabar linear
A. Pengertian sistem persamaan linear
Persamaan linier adalah suatu persamaan dengan n variabel yang tidak diketahui.
X1, X2, X3 ... , Xn yang dinyatakan dalam bentuk : a1 X1 + a2X2 + ... , an x n = b1
dimana a1, a2, ..., an dan b adalah kontanta real (kompleks).
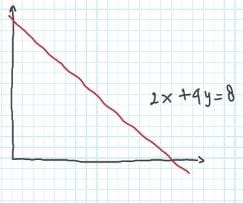
Persamaan linier secara geometri dengan istilah garis
Contoh :
Persamaan Linier :
(1). 2X1 + 4X2 = 10
(2). 2X1 - 4X2 + 3X3+4X4
Persamaan linier adalah suatu susunan yang terdiri dari m persamaan linier dan n variabel yang tidak diketahui yang berbentuk :
a11 X1 + a12 X2 + ... + a1n Xn = b1
a21 X1 + a22 X2 + ... + a2n Xn = b2
a31 X1 + a32 X2 + ... + a3n Xn = b3
a41 X1 + a42 X2 + ... + a4n Xn = b4
.............................................................
am 1x1 + am 2x2 + ... + amn x n = bm dimana X1, X2, ... , Xn disebut variable yang tidak diketahui, aij kontanta koefisien sistem persamaan linier dan bj kontanta yang diketahui.
B. Konsistensi SPL
Perhatikan contoh berikut
- Kasus 1 SPL berbentuk
- kasus 2n, SPL berbentuk
- kasus 3, SPL berbentuk :










Komentar
Posting Komentar