SIFAT-SIFAT DETERMINAN MATRIKS
Nama : Farahdiba soumena
Nim :202231006
Kelas : A
Jurusan : Teknik informatika
matkul : Aljabar linear
SIFAT-SIFAT DETERMINAN
2. jika A dan B adalah matrik bujur sangkar yang berordo sama maka
3. jika A matrik bujur sangkar yang memuat baris atau kolom dimana elemenya 0 atau sebanding , maka
det (A) = 0
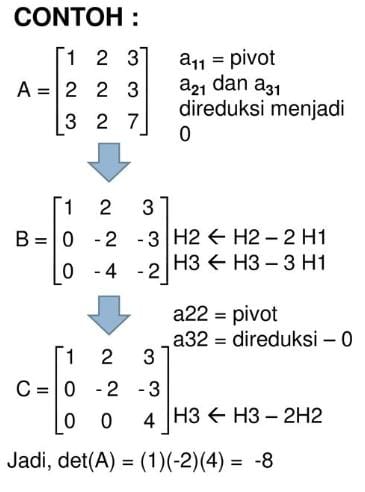
4. jika A matrik segitiga atas (bawah) yang berordo (nxn) dimana elemen diagonal utama tak nol , maka
5. jika A dan B matrik bujur sangkar yang berordo sama . jika matrik B diperoleh dari A dengan cara megalikan sembarangan baris (kolom) dengan konstanta K tak nol , maka
det (B) = K det (A)
6. jika A dan B matrik bujur sangkar yang berordo sama. jika matrik B diperoleh dari A dengan cara menukarkan semua elemen sembarangan baris (kolom), maka :
7. jika A dan B matrik bujur sangkar yang berordo sama. jika matrik B diperoleh dari A dengan cara mengalikan sembarangan baris (kolom) dengan konstanta K tak nol dan hasilnya dijumblahkan pada baris ( kolom) yang lain, maka :
Andaikan A matrik bujur sangkar berordo (nxn), Cij=(-1) i+j Mij kofaktor elemen matrik aij, dan andaikan pula det(A)=0 maka A mempunyai invers y
PENGERTIAN INVERS MATRIKS
AB = BA = I (matrik identitas)
B dikatakan invers matrik A ditulis A-1, maka :
A.A-1 = A-1.A
A dikatakan invers matrik B ditulis B-1 maka :
B-1.B = B.B-1
Contoh :
AB = BA = 1
Teknik Menghitung Invers
Metode adjoint matrik
Metode operasi elementer baris
Metode perkalian invers matrik elementer
Metode partisi matrik
Metode komputer MATCADS, MATLAB, WS OFFICE EXCEL
Metode Adjoint Matrik
Andaikan A matrik bujur sangkar berordo (nxn), Cij=(-1) i+j Mij kofaktor elemen matrik aij, dan andaikan pula det(A)=0 maka A mempunyai invers yaitu :












Komentar
Posting Komentar